In previous posts, we discussed the motivation for doing A/B testing on a product like Twitter, how A/B testing helps us innovate, and how DDG, our A/B testing framework, is implemented. Here we describe a simple technique for auto-detecting potentially buggy experiments: testing for unbalanced entry rates of users into experiment buckets.
Trigger analysis
An A/B test maps users to treatment “buckets.” The control bucket (“A”) is the current production experience; the treatment bucket (“B”) implements the change being tested. You can create multiple treatment buckets.
Choosing which bucket to show seems simple: randomly and deterministically distribute all user IDs over some integer space, and assign a mapping from that space to buckets.
But consider that many experiments change something only a subset of users will see. For example, we might want to change something about the photo editing experience on the iOS app — but not all of our users use iOS, and not all of the Twitter iOS users edit photos.
Including all users, regardless of whether they “triggered” the experiment or not, leads to dilution. Even if your feature changed something in the behavior of users who saw it, most did not, so the effect is hard to observe. It’s desirable to narrow the analysis by looking only at users who triggered the change. Doing so can be dangerous, however; conditionally opting people into the experiment makes us vulnerable to bias. Populations of different experiment buckets might not be comparable due to subtleties of the experiment setup, making results invalid.
A simple example
Let’s imagine an engineer needs to implement a US-specific experiment. She made sure that the treatment is not shown to users outside the US, using the following (pseudo-) code:
// bucket the user and record that the user is in the experiment
bucket = getExperimentAndLogBucket(user, experiment);
if (user.country == “US” && bucket == “treatment”) {
/** do treatment stuff **/
} else {
/** do normal stuff **/
}
This results in a diluted experiment, since users from all countries get recorded as being in either control and treatment, but only the US “treatment” users actually got to see the treatment.
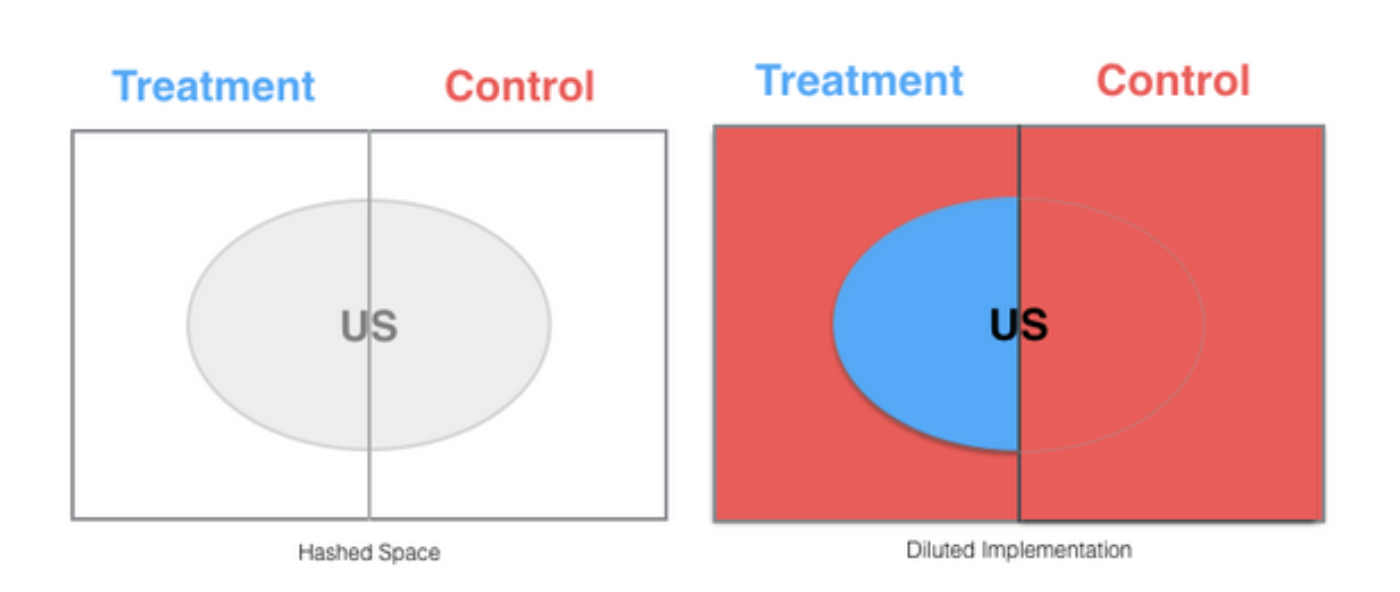
At this point, there is no bias — just dilution. When this is pointed out in code review, the code is changed as follows:
// bucket the user, but do not record triggering.
bucket = peekAtExperimentBucket(user, experiment);
if (user.country == “US” && bucket == “treatment”) {
recordExperimentTrigger(user, experiment, “treatment”)
/** do treatment stuff **/
} else {
if (bucket == “control”) {
recordExperimentTrigger(user, experiment, “control”)
}
/** do normal stuff **/
}
This new version looks like it will avoid the dilution problem, since it doesn’t record a bunch of people who didn’t see the treatment as having triggered it. It has a bug, however — there is bias in the experiment. Treatment only gets the US users, while control is seen as getting all the users. Nothing will break in the app, but the two buckets are not comparable.
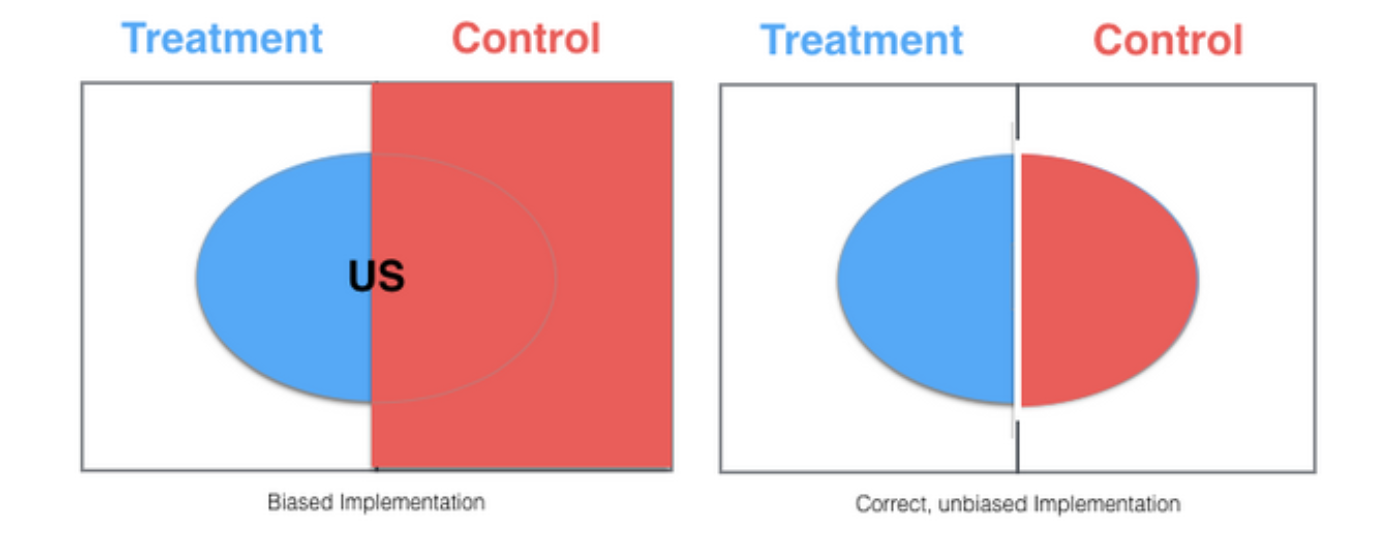
An unbiased solution would look as follows:
// bucket the user, but do not record triggering.
bucket = peekAtExperimentBucket(user, experiment);
if (user.country == “US” && bucket == “treatment”) {
recordExperimentTrigger(user, experiment, “treatment”)
/** do treatment stuff **/
} else {
// do not record trigger for non-US visitors, even in control
if (user.country == “US” && bucket == “control”) {
recordExperimentTrigger(user, experiment, “control”)
}
/** do normal stuff **/
}
Not all bucketing imbalances have such obvious causes. We recently encountered an experiment which triggered the user bucketing log call asynchronously, from client-side Javascript. The experimental treatment required loading certain additional assets and making other calls, which made the bucketing log call slightly less likely to succeed for users on slow connections. This resulted in bias: users on slow connections were more likely to show up in control than in treatment, subtly skewing the results.
Identifying bucket imbalance
An effective way to detect bucketing bias is to test for imbalanced bucket sizes. Our experimentation framework automatically checks if buckets are roughly the expected size, using two methods. First, we perform an overall health check using the multinomial goodness of fit test. This test checks if observed bucket allocations collectively matched expected traffic allocations. If overall health is bad, we also perform binomial tests on each bucket to pinpoint which buckets might have problems, and show a time series of newly bucketed users in case experimenters want to do a deep dive.
Overall health check using multinomial test
Imagine an experiment with k buckets, where bucket i receives p percent of the traffic (p can be different across buckets). Given that we know the total number of users who are bucketed into the experiment, we can model the number of users in each bucket jointly as a multinomial distribution. Furthermore, we can perform a goodness of fit test to see if the actual observed count deviates from the expected count. If we see that the traffic allocation deviates significantly from what it is supposed to be, this is a good indicator that split of traffic is problematic or that the splitting is biased.
Mathematically, the multinomial goodness of test is quite intuitive:
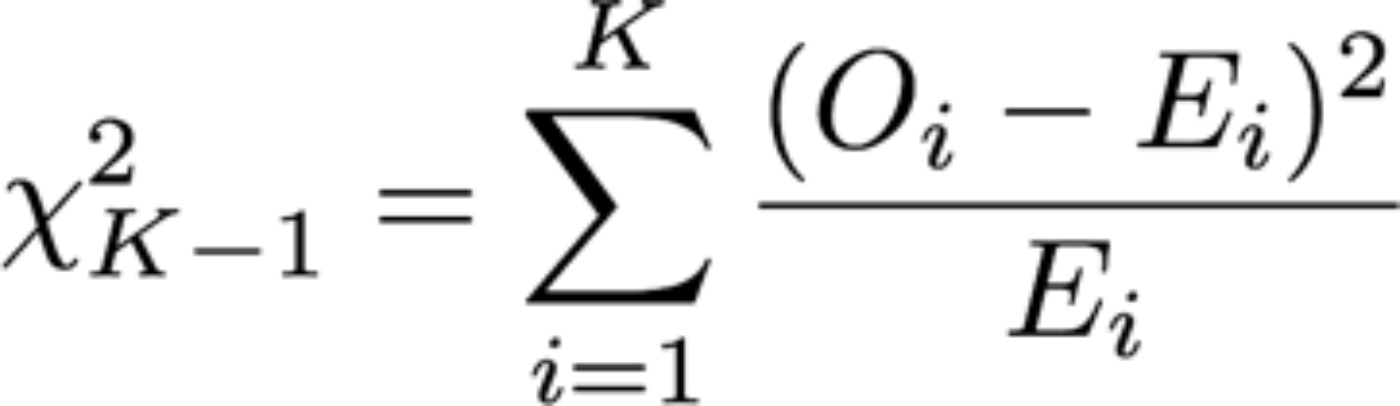
Here, O denotes the observed number of users bucketed in bucket i, and E denotes the expected number of users bucketed in each bucket. The statistics capture how much each bucket deviates from its expected value, and the summation captures the overall deviation. The test statistics follow a chi-square distribution (with k-1 degrees of freedom), so we can determine the likelihood of observing a deviation as large as in the current sample had the bucket allocation were to be defined by p’s.
It is worth noting that the multinomial test is a generalization of the binomial test (i.e. often used when there is only 1 control vs. 1 treatment group). In the past, we leveraged the binomial test so that each bucket was compared to its expected bucket count. However, in situations where an experiment has many buckets, we can quickly run into the problems of multiple hypothesis testing. Below, we plot the probability of getting at least one false positive as a function of the number of independent buckets, which is simply 1 - (1 - p)^k where p is the probability of a getting a false positive (often set at 5%). The increase in false positives rate in a properly designed experiment when multiple buckets are involved is fairly high: Under the null hypothesis, with 5 buckets, one would expect to see at least one of them be imbalanced more than 20 percent of the time.
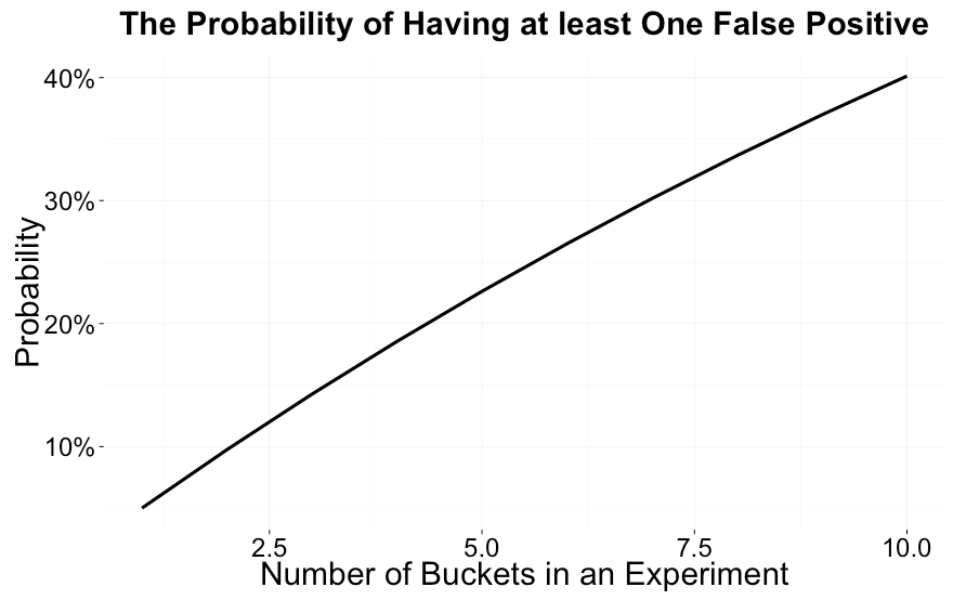
False positives lead to a lot of time spent in investigation, and loss of trust in the tool. To address this problem, we evaluated the improvement of switching from binomial test to multinomial.
We ran a meta-analysis using 179 experiments, and compared the bucket health results of multinomial and binomial tests. In the case of binomial, an experiment was considered unhealthy if at least one of the bucket has p-value < 0.05, while in the multinomial case, the experiment was labeled unhealthy if the overall p-value is < 0.05.
We found a subset of experiments where the binomial test concluded that the experiment is unhealthy while the multinomial test did not. We examined all such experiments, and observed that they shared some characteristics:
These characteristics suggested that the binomial results are likely to be false positives. We then verified that all of these experiments were set up correctly through manual validation. Switching to the multinomial test for overall health of the experiment reduced our false positive rate by an estimate of 25%.
Flagging individual buckets
The multinomial test can protect us from the woes of multiple hypothesis testing, but it has a disadvantage: it does not tell us which buckets are problematic. To provide more guidance, we run additional binomial tests in cases when the multinomial test flags an experiment.
DDG performs a two-sided binomial test using normal approximation of the binomial distribution.

The binomial test allows us to check if the traffic is roughly balanced at time t, and it flags abnormal buckets when the actual traffic is outside of the 95% confidence interval of the expected traffic.
Time series of bucket count
At the lowest level of granularity, our tool also presents the time series of bucket count in an 8 hour batch time window. Below are two examples: a healthy time series, and an unhealthy one.
Example 1: healthy time series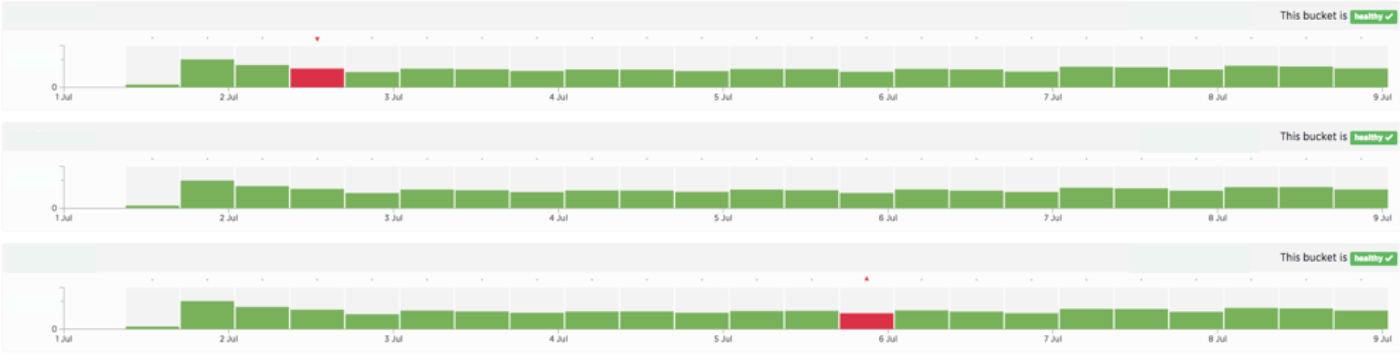
In the above example, the time series indicates that the number of users in each bucket are balanced across buckets, except a few batches (the color labeling again is determined based on binomial test, at each time t). The two unbalanced batches are not concerning: with the significance level set at 5%, we would expect a false positive 1 out of every 20 tests. The multinomial test is not significant. Overall, we see no evidence for biased bucketing.
Example 2: unhealthy time series
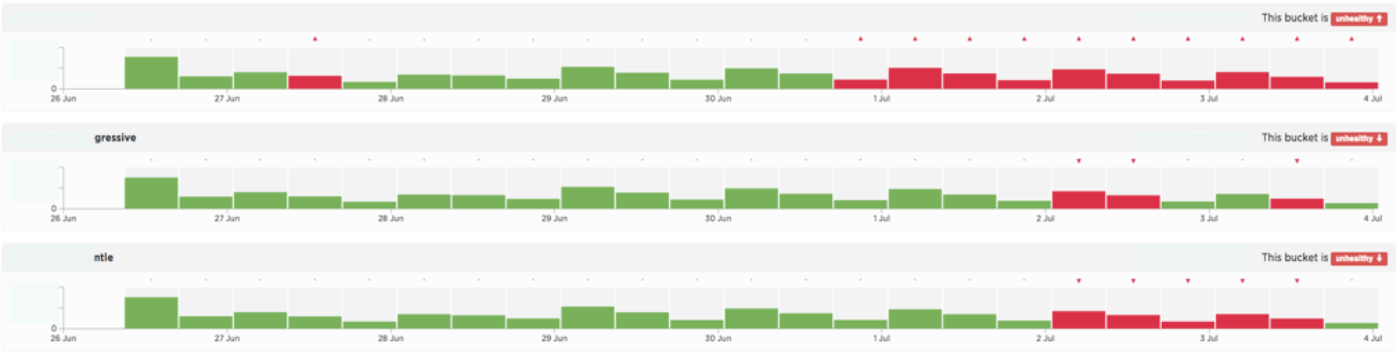
In this example, we see that a few days after the experiment started, the number of new users started to deviate from the expected traffic, indicating bucketing bias. Looking at the overall bucket health (top right), we also see that the multinomial test indicates that the test is unhealthy. In this case, the tool warns the user to investigate the design before moving to analysis.
This combination of batch-level and global testing allows us to detect more subtle problems than either type of test would detect individually.
Test only on users, not impressions
A properly designed and implemented experiment can have the total number of bucketed impressions vary across buckets due to experiment effects or implementation details. Comparing bucket imbalance based on unique bucketed users is a better test than looking at total triggers or total visits.
It is important to note that in our time series tests, we check bucket imbalance on users bucketed for the first time instead of all bucketing events. The experiment itself can cause users to continue triggering the experiment, or to do so less than control. This makes post-exposure impression data inappropriate to compare. In the overall test, we also only compared total number of users bucketed, rather than total impressions scribed across buckets.
Conclusion
The bucket imbalance check is a powerful, yet simple and convenient way to determine if an experiment might not be set up correctly. This is the very first thing we check to validate experiment results, and building it into our toolchain helped save many hours of investigation and analysis. By automatically checking experiments for clear evidence of bias, we drastically reduce time required to detect a problem and increase the experimenters’ confidence in experiment results.
Did someone say … cookies?
X and its partners use cookies to provide you with a better, safer and
faster service and to support our business. Some cookies are necessary to use
our services, improve our services, and make sure they work properly.
Show more about your choices.